Scan Conversion Scan Conversion merupakan metoda untuk memetakan titik ke dalam suatu pixel. Scan Conversion dapat dilakukan terhadap Line (garis), polygon, ataupun garis lengkung (kurva) yang terdiri dari beberapa teknik untuk mengubah vertikal / horizontal frekuensi scan dari sinyal video untuk tujuan dan penerapan yang berbeda.
Berhubungan dengan pembuatan garis pada Scan Conversion terdiri dari beberapa Algoritma yang dibutuhkan, seperti :
Setelah beberapa Algoritma yang di butuhkan dalam pembentukan garis di Scan Conversion yang telah saya sampaikan tadi, saya akan mengulas salah satu cara penggabaran garis dengan menggunakan metoda Algoritma Bresenham, yaitu :
Selain adanya teknik penggambaran garis, di dalam Scan Conversion dikenal juga teknik penggabungan garis (Joining), seperti Ugly, Bevel, Round, Miter. Berikut merupakan gambar dari teknik penggabungan dua garis dengan tipe Ugly, Bevel, Round, dan Miter.


TransformationsTransformation adalah suatu metoda untuk mengubah lokasi titik. Operasi-Operasi Primitive pada Transformations terbagi menjadi:
Berikut ini merupakan contoh dari gambar pembentukan suatu objek masing-masing:
Dalam transformasi linear, metoda pengubahan lokasi titik dilakukan secara teratur, dan membentuk semacam pattern. Misalnya dalam grafik 2 dimensi, transformasi linear melakukan penambahan atau pengurangan garis lurus secara teratur. Berikut merupakan contoh transformasi linear :

Sedangkan transformasi non linear adalah metoda pengubahan lokasi titik yang tidak dilakukan secara teratur. Dalam grafik, pengurangan atau penambahan garis yang dilakukan tidak akan membentuk sebuah pattern yang teratur. Contoh transformasi non linear :

Di dalam teknik Tranformasion terdapat beberapa contoh Linear Transformation dan Non-Linear Transformation dari Operasi-Operasi Primitive transformation! Contoh operasi primitive

Perbedaan antara Geometric Transformation dan Color Space Transformation adalah dalam transformasi geometric perubahan titik lebih memfokuskan pada bentuk dari objek yang berubah tersebut. Sedangkan Color space transformation lebih menitik beratkan pada perubahan warna dari titik-titik pixel tersebut.
Sistem koordinat homogen adalah system koordinat yang mempunyai satu dimensi lebih tinggi dari system koordinat yang ditinjau. Digunakan untuk menyatakan semua proses transformasi dengan perkalian matrix termasuk pergeseran.
Proyeksi merupakan salah satu jenis transformasi, yaitu transformasi koordinat. Proyeksi pada bidang datar (planar) dilakukan melalui sinar proyeksi yang muncul dari titik pusat proyeksi melewati setiap titik dari benda dan memotong bidang proyeksi (projection plane) untuk mendapatkan benda hasil proyeksi. Proyeksi Planar (Planar Geometric Projections) dibedakan menjadi:



Sekian informasi yang dapat saya sampaikan melalui Tugas Pengantar Teknologi Game yang pertama, mohon maaf apabila ada kesalahan. Terimakasih.
Sumber :

Berhubungan dengan pembuatan garis pada Scan Conversion terdiri dari beberapa Algoritma yang dibutuhkan, seperti :
- Algoritma DDA, adalah suatu algoritma (pendekatan) pengkonversian suatu himpunan pixel–pixel menjadi suatu garis yang didasari atas perhitungan delta(x) dan delta(y),
- Algoritma Bresenham merupakan suatu algoritma (pendekatan) yang dikreasikan oleh Bresenham yang tidak kalah akurat dan efisien dengan algoritma primitif lainnya (seperti DDA), bagian pengkonversian (scan–konversi) garis akan melakukan kalkulasi untuk penambahan nilai–nilai integer (yang dibutuhkan untuk membentuk garis) yang disesuaikan dengan tipe grafik yang dipakai oleh layar komputer,
- Algoritma C++.
Setelah beberapa Algoritma yang di butuhkan dalam pembentukan garis di Scan Conversion yang telah saya sampaikan tadi, saya akan mengulas salah satu cara penggabaran garis dengan menggunakan metoda Algoritma Bresenham, yaitu :
- ALGORITMA GARIS BRESSENHAM Prosedur untuk menggambar kembali garis dengan membulatkan nilai x atau y ke bilangan integer memerlukan waktu. serta variabel x,y maupun m memerlukan bilangan real karena kemiringan merupakan nilai pecahan. Bressenham mengembangkan algoritma klasik yang lebih menarik, karena hanya menggunakan perhitungan matematik dengan bantuan bilangan integer. Dengan demikian tidak perlu membulatkan nilai posisi pixel setiap waktu. Langkah-langkahnya adalah sebagai berikut:
- Tentukan dua titik yang akan dihubungkan dalam pembentukan garis
- Tentukan salah satu titik disebelah kiri sebagai titik awal (x0,y0) dan titik lainnya sebagai titik akhir (x1,y1)
- Hitung dx, dy, 2dx dan 2dy-2dx
- Hitung parameter P0 = 2dy – dx
- Untuk setiap xk sepanjang garis dimulai dengan k=0 § Bila Pk < 0 maka titik selanjutnya adalah (xk+1, yk) dan Pk+1=Pk+2dy § Bila tidak maka titik selanjutnya adalah (xk+1, yk+1) dan Pk+1=Pk+2dy-2dx
- Ulangi poin ke 5 untuk menentukan posisi pixel selanjutnya sampai x=x1 dan y=y1
Dalam pembentukan garis dalam penerapan materi Scan Conversion, ada beberapa hal yang juga harus kita perhatikan dalam menggambarkan garis, seperti ketebalan garis (thickness) dan juga Bentuk tepi garis (ends) yang terdiri dari : Butt, Round dan Square. Berikut merupakan gambar dengan bentuk tepi Butt, Round dan Square.

Selain adanya teknik penggambaran garis, di dalam Scan Conversion dikenal juga teknik penggabungan garis (Joining), seperti Ugly, Bevel, Round, Miter. Berikut merupakan gambar dari teknik penggabungan dua garis dengan tipe Ugly, Bevel, Round, dan Miter.
- Mitter >> titik pertemuan 2 garis lurus yang membentuk sudut lancip
- Round >> titik sudut pertemuan yang membulat
- Bevel >> titik sudut pertemuannya tampak terpotong rata
- None >> titik sudut pertemuan yang terpotong agak membentuk siku
- Type Ugly Joined Line

- Type Miter, Square dan Bevel Join

TransformationsTransformation adalah suatu metoda untuk mengubah lokasi titik. Operasi-Operasi Primitive pada Transformations terbagi menjadi:
- Scale
- Rotate
- Shear
- Flip
- Translate
Berikut ini merupakan contoh dari gambar pembentukan suatu objek masing-masing:
- Scale merupakan skala pengali sama untuk semua komponen.

- Rotate merupakan adalah merotasi atau memutar suatu objek dengan nilai yang ditentukan. Dibawah ini adalah Rotasi terhadap titik (0,0) sebanyak 450 .
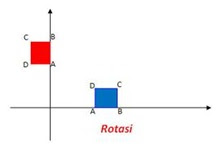
- Translasi (Perpindahan)

- Pencerminan (Flip)

- Shear

Dalam transformasi linear, metoda pengubahan lokasi titik dilakukan secara teratur, dan membentuk semacam pattern. Misalnya dalam grafik 2 dimensi, transformasi linear melakukan penambahan atau pengurangan garis lurus secara teratur. Berikut merupakan contoh transformasi linear :

Sedangkan transformasi non linear adalah metoda pengubahan lokasi titik yang tidak dilakukan secara teratur. Dalam grafik, pengurangan atau penambahan garis yang dilakukan tidak akan membentuk sebuah pattern yang teratur. Contoh transformasi non linear :

Di dalam teknik Tranformasion terdapat beberapa contoh Linear Transformation dan Non-Linear Transformation dari Operasi-Operasi Primitive transformation! Contoh operasi primitive

Perbedaan antara Geometric Transformation dan Color Space Transformation adalah dalam transformasi geometric perubahan titik lebih memfokuskan pada bentuk dari objek yang berubah tersebut. Sedangkan Color space transformation lebih menitik beratkan pada perubahan warna dari titik-titik pixel tersebut.
Sistem koordinat homogen adalah system koordinat yang mempunyai satu dimensi lebih tinggi dari system koordinat yang ditinjau. Digunakan untuk menyatakan semua proses transformasi dengan perkalian matrix termasuk pergeseran.
Proyeksi merupakan salah satu jenis transformasi, yaitu transformasi koordinat. Proyeksi pada bidang datar (planar) dilakukan melalui sinar proyeksi yang muncul dari titik pusat proyeksi melewati setiap titik dari benda dan memotong bidang proyeksi (projection plane) untuk mendapatkan benda hasil proyeksi. Proyeksi Planar (Planar Geometric Projections) dibedakan menjadi:
- Proyeksi Paralel. Berdasarkan hubungan antara arah proyeksi dengan vektor normal dari bidang proyeksi, proyeksi paralel dibedakan menjadi:
- Orthographic Proyeksi orthographic ada yang disebut proyeksi axonometric. Proyeksi Axonometric dibedakan menjadi proyeksi:
- isometric
- dimetric
- trimetric.
- Oblique.
- Proyeksi Perspektif. Perbedaan antara proyeksi parallel & perspektif adalah: pada proyeksi parallel jarak antara titik pusat proyeksi ke bidang proyeksi tidak terhingga, sementara para proyeksi perspektif jarak antara titik pusat proyeksi ke bidang proyeksi bersifat infinite (tertentu).
- Proyeksi Orthographic diperoleh apabila sinar proyeksi tegak lurus dengan bidang proyeksi. Proyeksi orthographic sering digunakan untuk menghasilkan tampak depan, tampak belakang, tampak samping dan tampak atas dari sebuah benda atau disebut sebagai Multiview orthographic. Tampak atas, tampak belakang dan tampak dari samping sebuah benda sering disebut sebagai elevation. Sedangkan tampak dari atas disebut sebagai plan view. Transformasi untuk proyeksi multiview orthographic dapat diperoleh dengan rumus Proyeksi terhadap bidang x-z:qx = px,qy =pz Proyeksi terhadap bidang y-z:qx = px,qy =pz Proyeksi terhadap bidang x-y:qx = px,qy =py Dimana q(x,y) merupakan titik hasil proyeksi dari p(x,y,z) seperti digambarkan di bawah ini :

- Proyeksi orthographic yang menampakan lebih dari satu permukaan benda disebut sebagai proyeksi axonometric
- proyeksi axonometric dilakukan dengan mengatur agar bidang proyeksi berpotongan dengan ketiga sumbu koordinat (principal axes) pada sudut yang sama maka kita akan memperoleh proyeksi isometric
- proyeksi dimetric yaitu proyeksi yang diperoleh dengan mengatur agar bidang proyeksi berpotongan dengan dua sumbu utama pada sudut yang sama
- proyeksi trimetric diperoleh apabila ketiga sumbu utama berpotongan dengan bidang proyeksi pada sudut yang berbeda

- Proyeksi Perspective Proyeksi Perspective diperoleh saat sudut pandang yang lebih realistis dibandingkan proyeksi orthographic. Pada kenyataannya jarak benda terhadap kita akan mempengaruhi bagaimana benda tersebut terlihat. Benda yang terlihat jauh akan kelihatan kecil sedangkan benda yang dekat akan terlihat lebih besar. Efek ini disebut sebagai shortening. Pada perspektif semua garis menghilang pada satu atau lebih titik yang sama atau disebut titik hilang (vanishing point). Contoh dari proyeksi perspektif :

- Perbedaan antara proyeksi parallel & perspektif secara umum ialah pada proyeksi parallel jarak antara titik pusat proyeksi ke bidang proyeksi tidak terhingga, sementara para proyeksi perspektif jarak antara titik pusat proyeksi ke bidang proyeksi bersifat infinite (tertentu). Dalam penggunaan kedua teori ini terdapat beberapa perbedaan yang dapat dilihat dari tabel perbandingan yang ada seperti di bawah ini :

Sekian informasi yang dapat saya sampaikan melalui Tugas Pengantar Teknologi Game yang pertama, mohon maaf apabila ada kesalahan. Terimakasih.
Sumber :
- http://dazako.blogspot.com/2009/05/transformasi-obyek-dua-dimensi.html
- http://www.mathworks.com/matlabcentral/fileexchange/28790-colorspace-transformations https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=0CC4QFjAA&url=http%3A%2F%2Finst.eecs.berkeley.edu%2F~cs184%2Ffa05%2Flectures%2Flecture- 03.pdf&ei=jfFlUdm5ObCuiQf2tYCwBA&usg=AFQjCNF5mydLIEOwhMZdJLTd_oyt_-3stA&sig2=BF12NPxbZ92pVMtnK8c62A&bvm=bv.45107431,d.aGc&cad=rja
- http://harmon-middle-school.wikispaces.com/Linear+and+Nonlinear+Graphs!!!
- http://fellypun.wordpress.com/2013/01/15/80/
- http://prihastomo.wordpress.com/2011/01/17/konversi-scan/

Tidak ada komentar:
Posting Komentar